Decimal to Binary Conversion Example (20.1.6)
To help understand the process, consider the IP address 192.168.11.10.
The first octet number 192 is converted to binary using the previously explained positional notation process.
It is possible to bypass the process of subtraction with easier or smaller decimal numbers. For instance, notice that it is fairly easy to calculate the third octet converted to a binary number without actually going through the subtraction process (8 + 2 = 10). The binary value of the third octet is 00001010.
The fourth octet is 11 (8 + 2 + 1). The binary value of the fourth octet is 00001011.
Converting between binary and decimal may seem challenging at first, but with practice it should become easier over time.
Figures 20-11 through 20-21 illustrate the conversion of the IP address of 192.168.10.11 into binary.
In Figure 20-11, is the first octet number 192 equal to or greater than the high-order bit 128?
• Yes it is, therefore add a 1 to the high-order positional value to a represent 128.
• Subtract 128 from 192 to produce a remainder of 64.
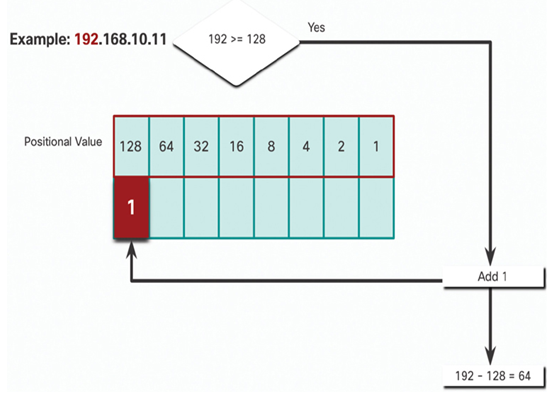
Figure 20-11 Step 1
In Figure 20-12, is the remainder 64 equal to or greater than the next high-order bit 64?
• It is equal, therefore add a 1 to next high-order positional value.
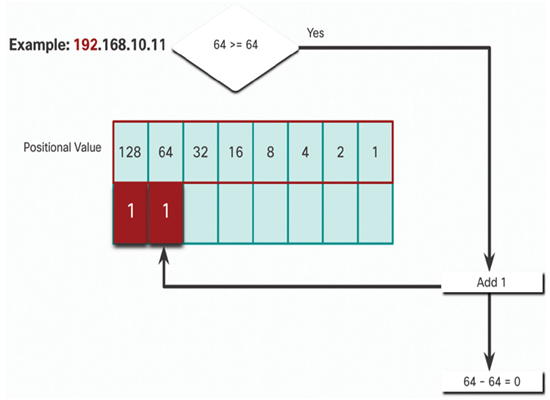
Figure 20-12 Step 2
In Figure 20-13, since there is no remainder, enter binary 0 in the remaining positional values.
• The binary value of the first octet is 11000000.
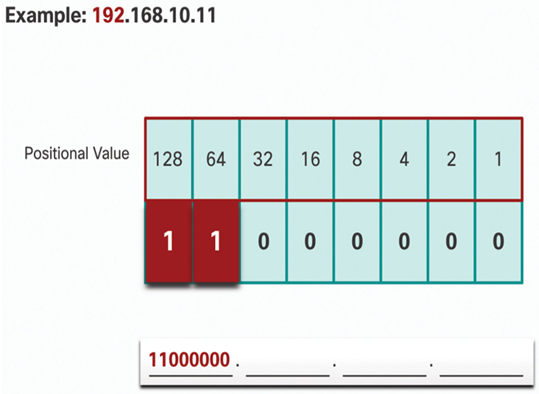
Figure 20-13 Step 3
In Figure 20-14, is the second octet number 168 equal to or greater than the high-order bit 128?
• Yes it is, therefore add a 1 to the high-order positional value to represent 128.
• Subtract 128 from 168 to produce a remainder of 40.
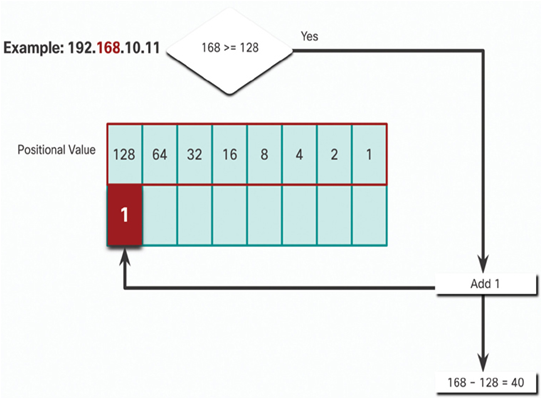
Figure 20-14 Step 4
In Figure 20-15, is the remainder 40 equal to or greater than the next high-order bit 64?
• No it is not, therefore, enter a binary 0 in the positional value.
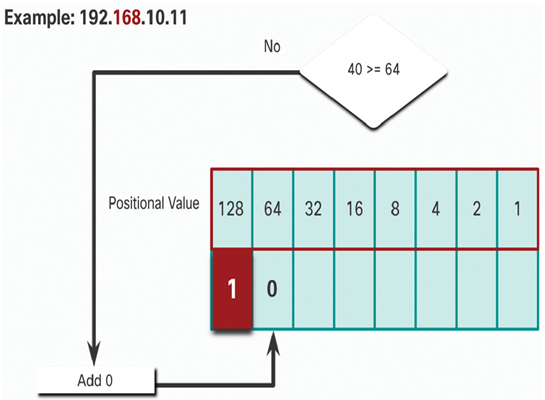
Figure 20-15 Step 5
In Figure 20-16, is the remainder 40 equal to or greater than the next high-order bit 32?
• Yes it is, therefore add a 1 to the high-order positional value to represent 32.
• Subtract 32 from 40 to produce a remainder of 8.
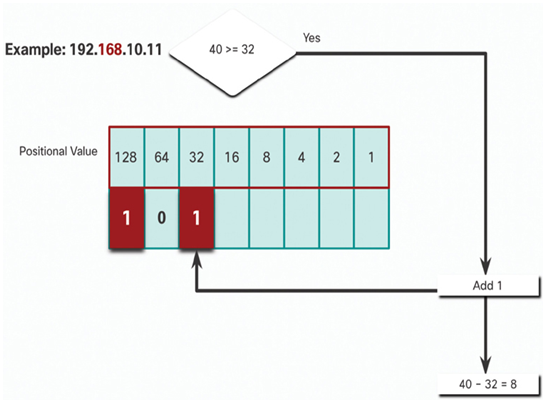
Figure 20-16 Step 6
In Figure 20-17, is the remainder 8 equal to or greater than the next high-order bit 16?
• No it is not, therefore, enter a binary 0 in the positional value.
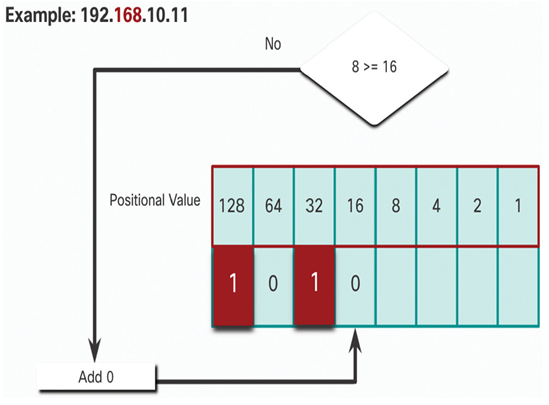
Figure 20-17 Step 7
In Figure 20-18, is the remainder 8 equal to or greater than the next high-order bit 8?
• It is equal, therefore add a 1 to next high-order positional value.
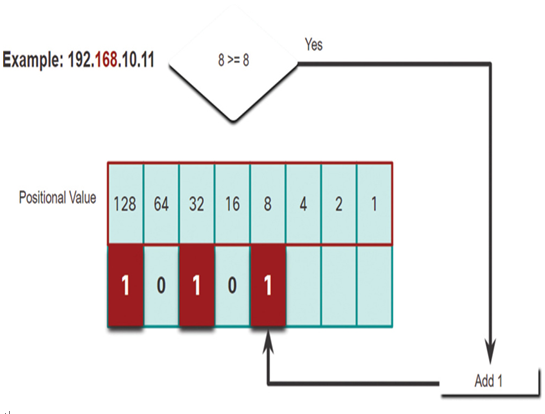
Figure 20-18 Step 8
In Figure 20-18, since there is no remainder, enter binary 0 in the remaining positional values.
• The binary value of the second octet is 10101000.
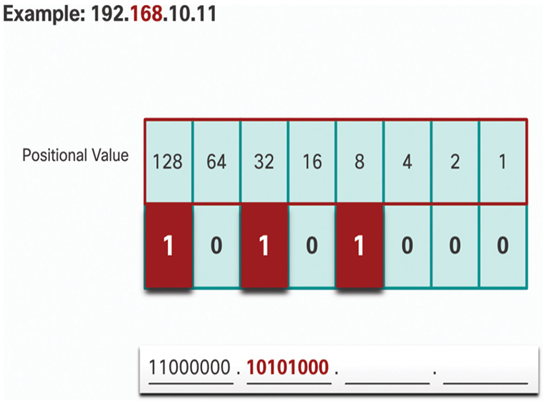
Figure 20-19 Step 9
In Figure 20-20, the binary value of the third octet is 00001010.
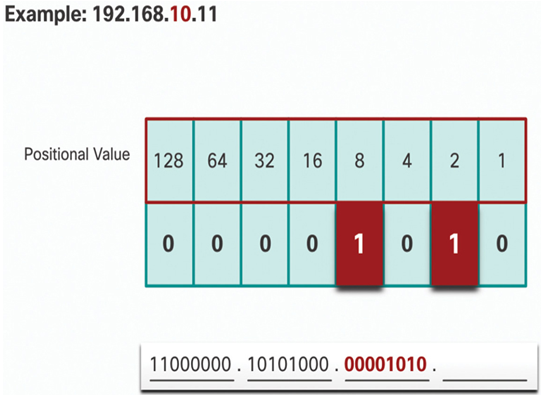
Figure 20-20 Step 10
In Figure 20-21, the binary value of the fourth octet is 00001011.
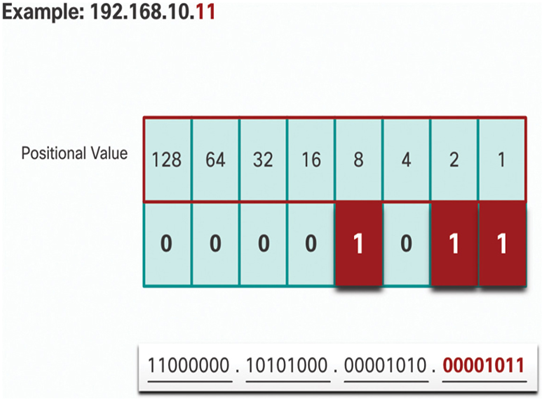
Figure 20-21 Step 11
